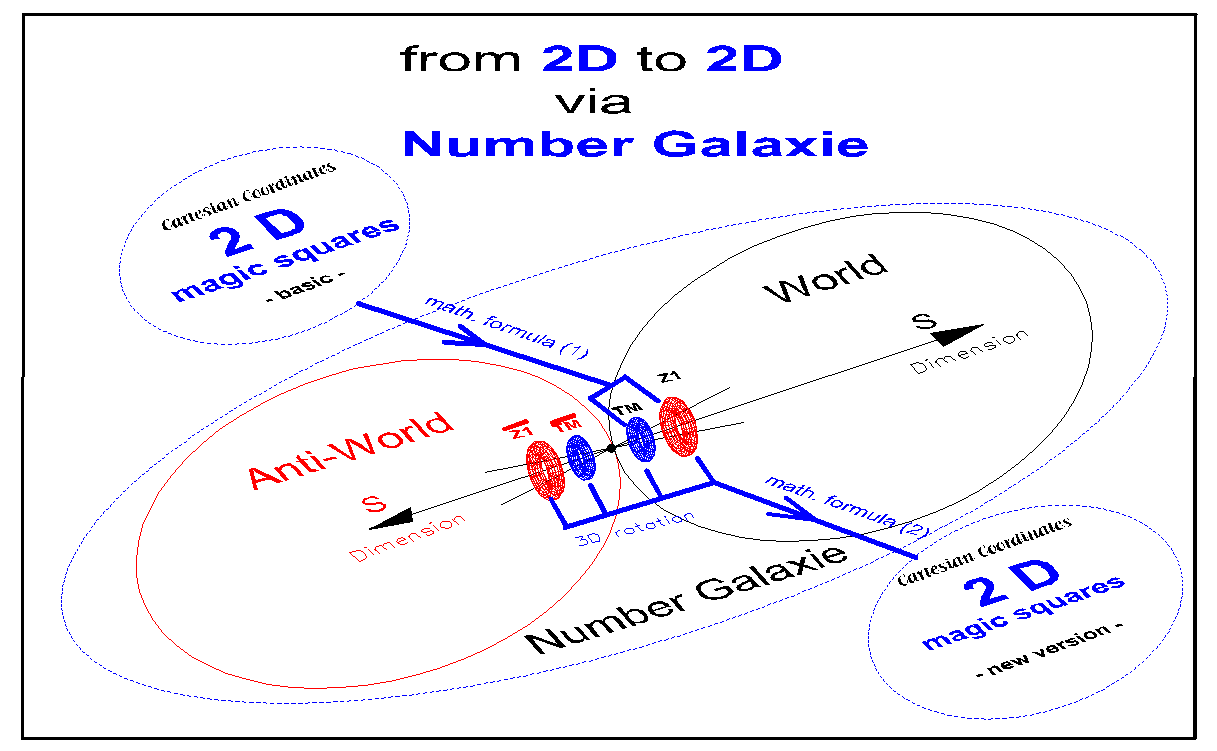
String theory in physics is still unfortunately a theory but already applied in the mathematics of multidimensional magic squares here. If in the natural numbers you introduce definition "world" and "antiworld", then these natural numbers fall apart on rotating and swinging strings. |
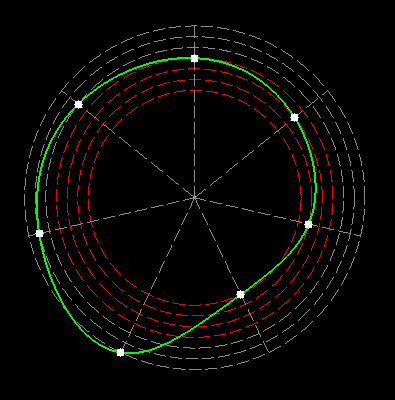
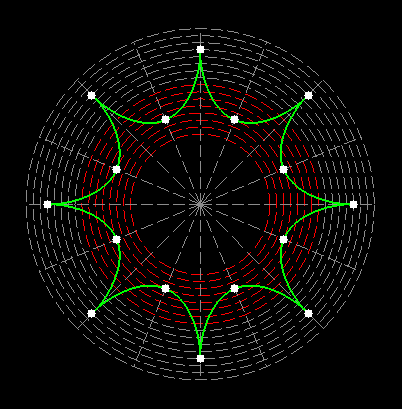
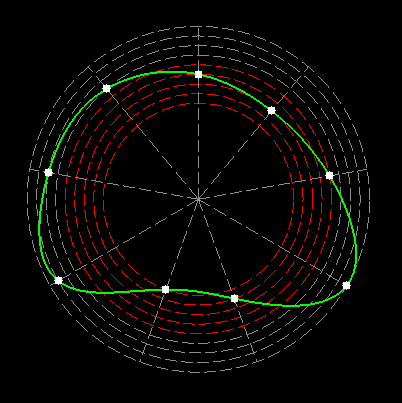
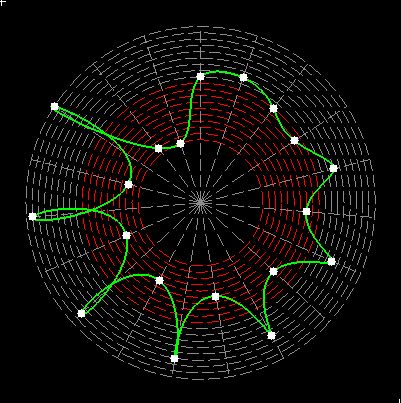
The numbers inscribed in a multidimensional magic figure (array) are the result of the sum of rotating, closed curves in the polar system. These numbers do not change their position and behave as if they were a standing wave. If the equivalent in the structure of the atom are rotating, hypothetical strings, then the result is matter as a standing wave. |
link: Why the model is called Number Galaxy ? | Notes: Graphics shown below are links. Please click on it and scroll down. There are beautiful dynamic graphics shown. |
| Are there similarities between galaxies, black holes and magic squares? |
Answer of organisation stars@stsci.edu ticket INC0212881 among others space telescope images: All Webb space telescope images are in the public domain, so, yes, you already have permission!
You may use them in any way you want, as long as what you are doing is legal and otherwise permitted. Content you may pick up and reuse includes the following among others: space telescope images.
 |
 |
 |
| three arm galaxy | TM-string and in the center 3D bordered prime magic square | spiral galaxy and black hole |
| Photo from James WEBB spaces telescopes comparison with magic square |
 |
 |
 |
 |
simple magic square inlaid group 1 of order 69 | pandiagonal ultramagic square of order 33 |
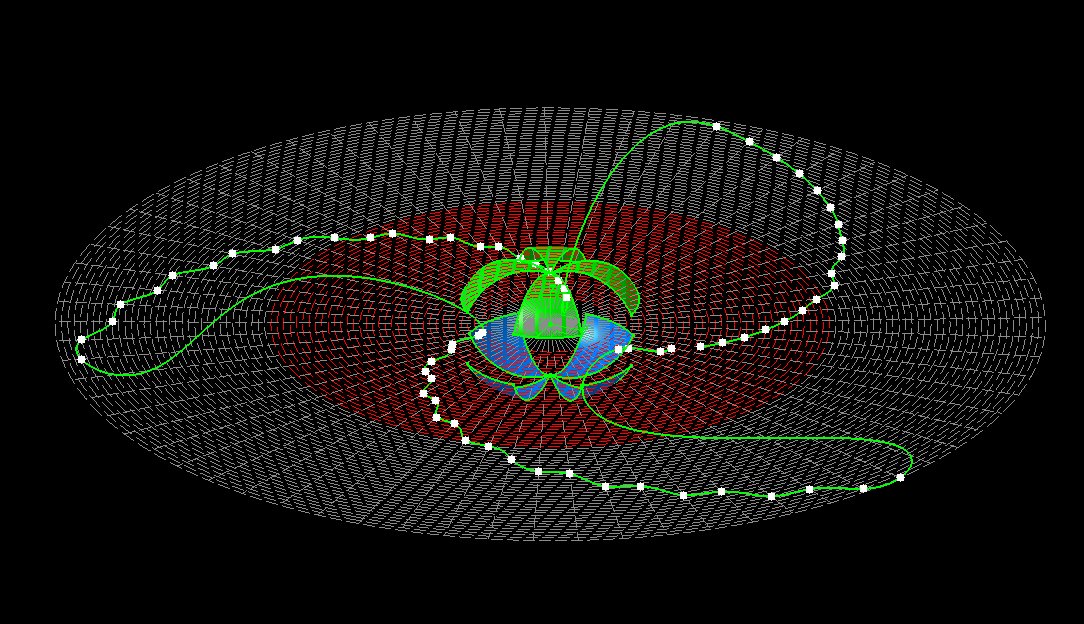
| Are parallels in the multiverse in astrophysics and in multidimensional magic squares? |
The concept of the multiverse has gained increasing importance in recent times, especially after the results of the James WEBB Space Telescope and finally in science. Recent computer calculation results in the field of multidimensional magical figures show astonishing parallels |
 |
 |
 |
| suspected multiversum in astrophysics | theoretically parallel universes in astrophysics | parallel universes in multidimensional magic squares |
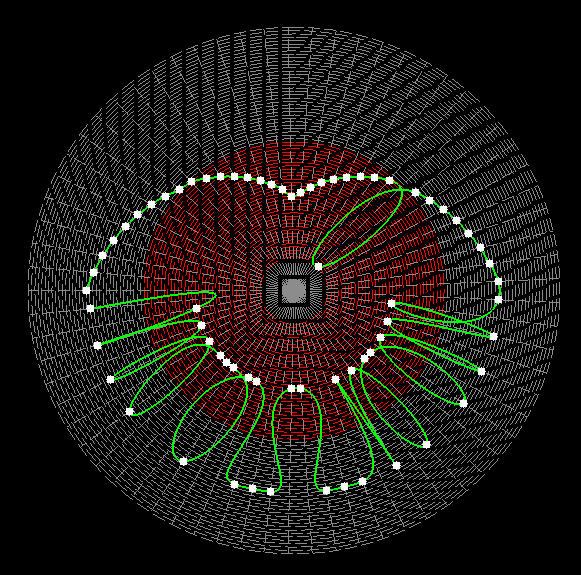
| Are parallels in the symmetry in physics and in multimagic squares? |
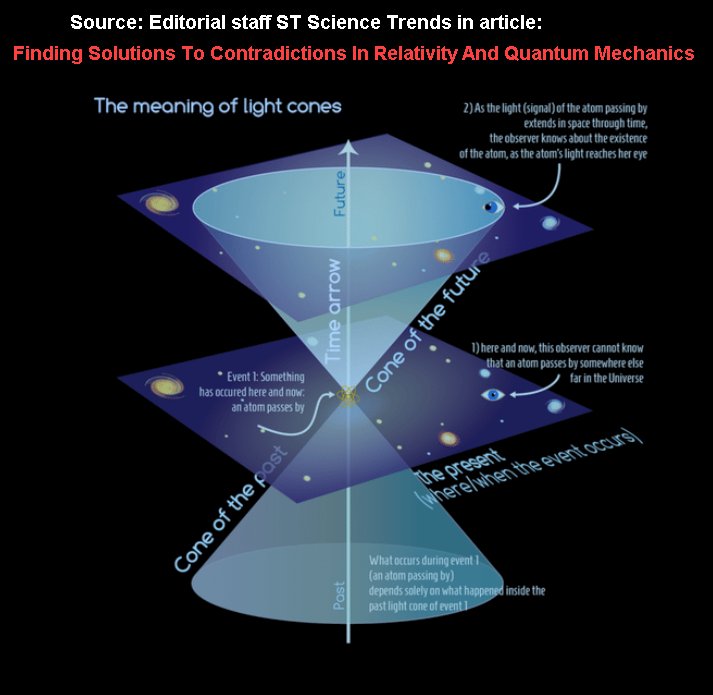
The symmetry of an object is its reflection, which means that in the mirror the image of the object is reversed. |
 |
 |
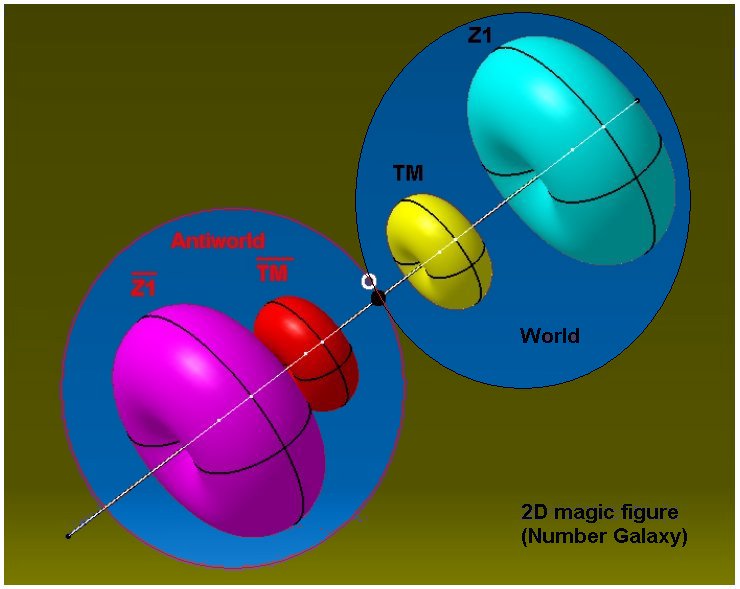 |
| Causal structure of spacetime in the form of light cones | Symmetry in 2D magic squares | World and antiworld concept in the magic squares |
| In this section of my website I will not present a new mathematical theory in the area of prime numbers, but rather show the results of computer calculations of magic squares of prime numbers in a different light. It's about the prime numbers that are built into so-called bordered magic squares with the help of AI programming. The prime numbers form the set with the following properties: p1 + p2 = 2✖c notic: p1 and p2 - prime numbers, c - middle number as an integer, ✖ multiplication sign. The computer program builds the magic square from the center of the square outwards. What's very interesting is that the prime numbers built in this way lie on a paraboloid-like surface in a three- dimensional coordinate system. What does this have in common with the Riemann Zeta function? In the zeta function, all non-trivial zeros lie on the critical line Re = 0,5. Here, the upper function p1 + p2 = 2✖c can be represented differently, namely: c / (p1+p2) = 0,5. Visualization of dynamic processes please click on the graphics below, scroll and open the video file in mp4 format. |
3D rotation of prime magic square order 29 and non prime magic square order 157 |
||
|
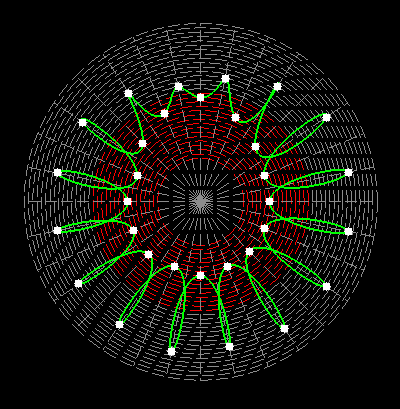
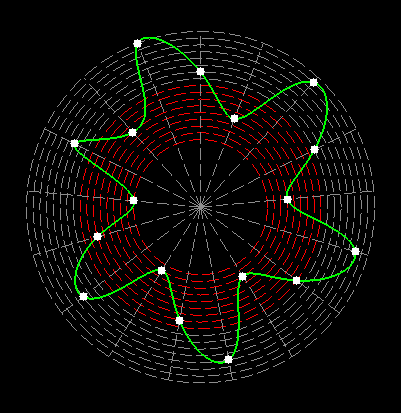
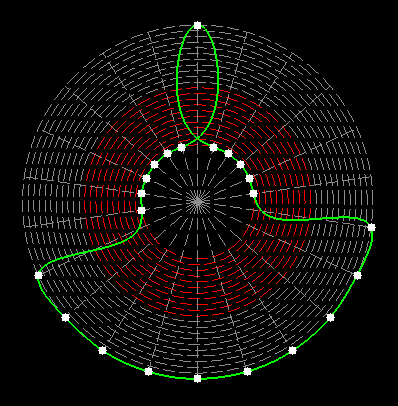
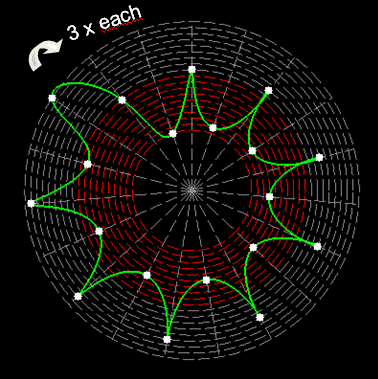
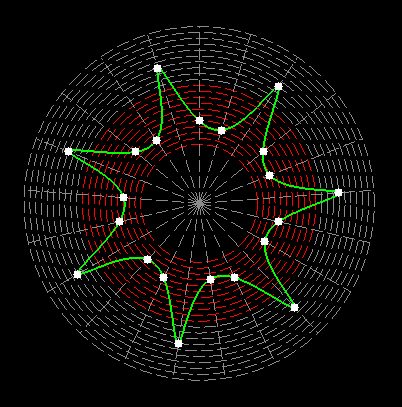
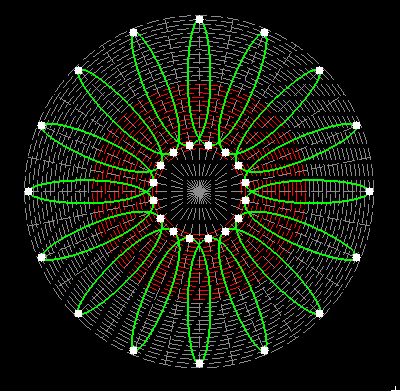
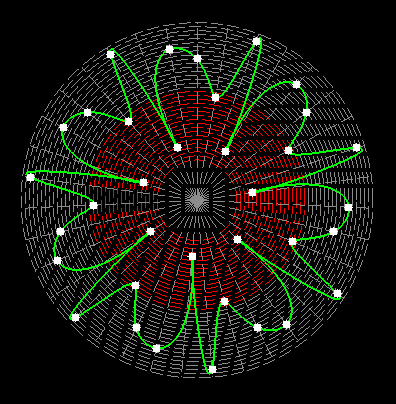
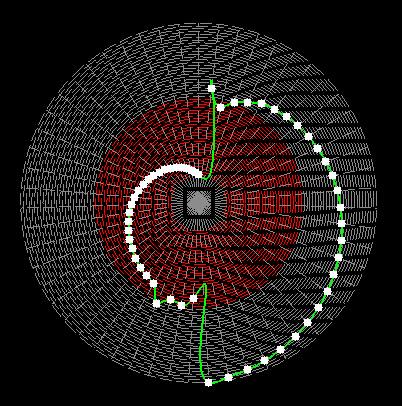
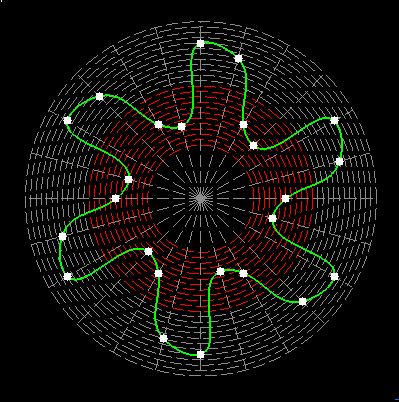
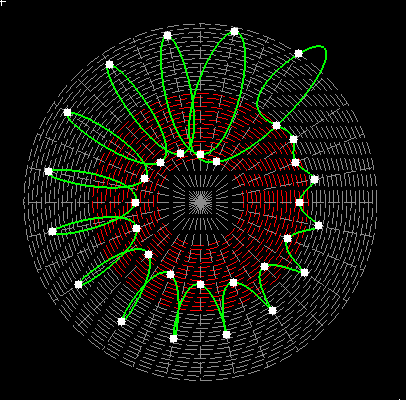
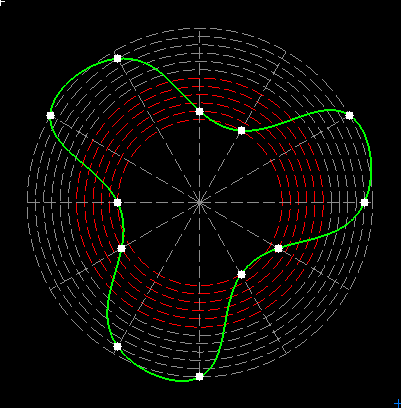
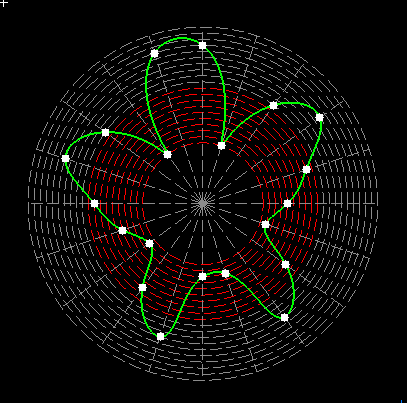
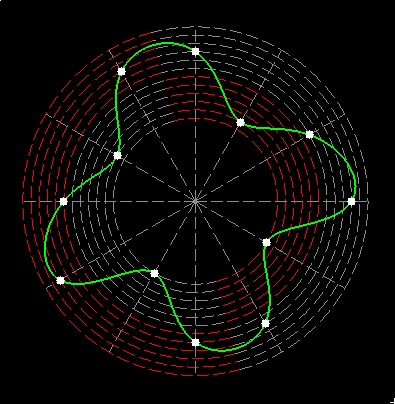
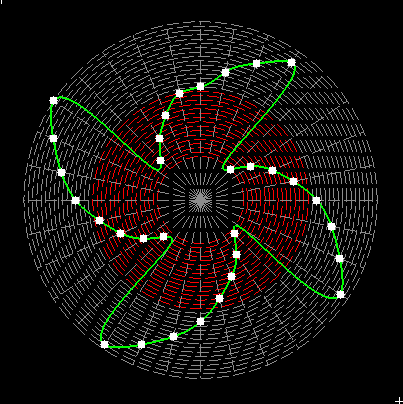
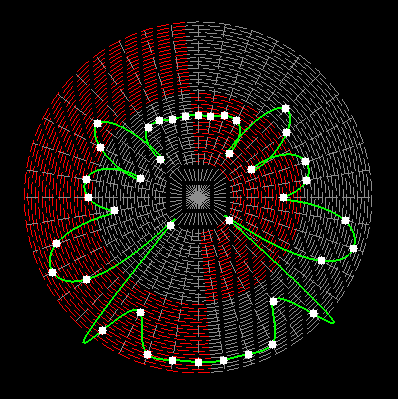
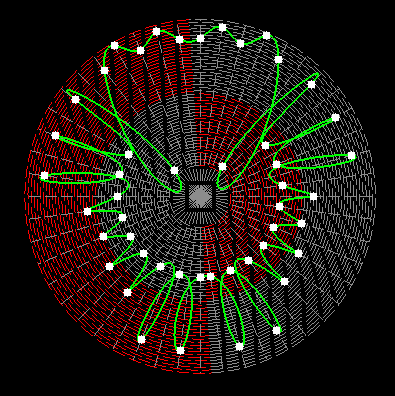
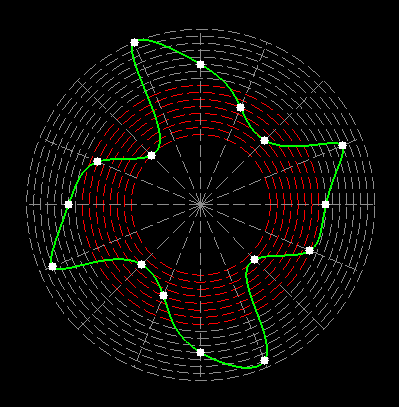
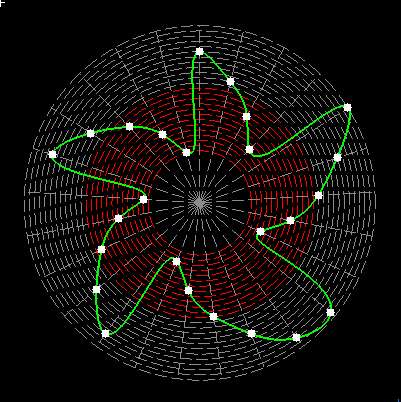
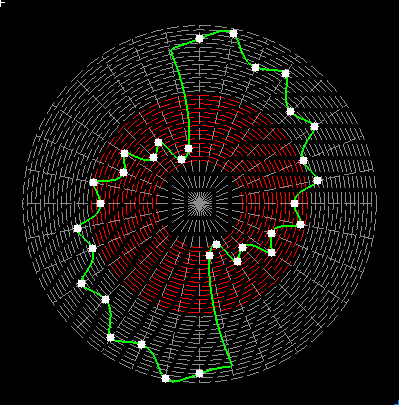
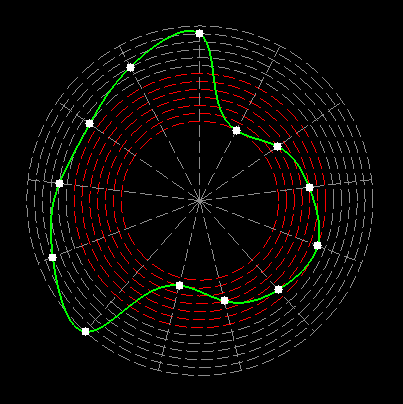
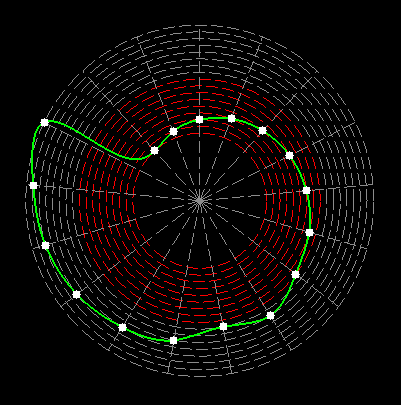
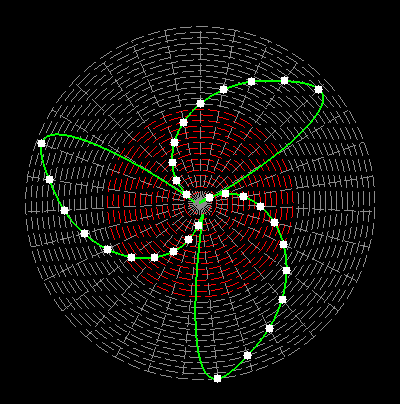
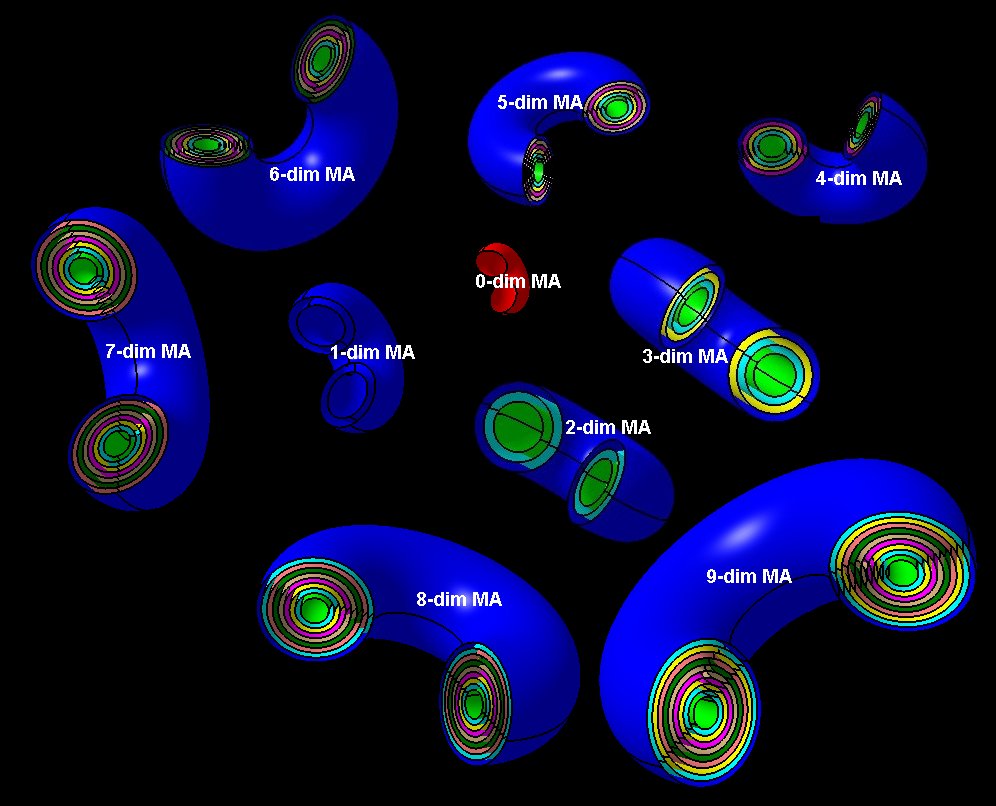
Here on my website, I will not present a new mathematical theory, but rather present the results of computer calculations of magic figures in a different light, based on dynamic visualization in a system mathematically similar to the polar system. The difference here lies in the introduction of positive and negative area (world and antiworld) in the polar system. The plotted points in this polar system are connected by one-dimensional lines called splines, very similar to the concept of strings introduced in physics. The examples presented here of magic squares and cubes with different properties (simple, pandiagonal, bimagic, trimagic) can be computer-decomposed according to the formula: magic squares (2 dim.): MA = TM✖N + 1 - Z1 magic cubes (3 dim.): (MA = TM✖N + 1 - Z1)✖N + 1 - Z2 magic tesseracts (4 dim.): ((MA = TM✖N + 1 - Z1)✖N + 1 - Z2)✖N + 1 - Z3 magic Hipercube (5 dim.): (((MA = TM✖N + 1 - Z1)✖N + 1 - Z2)✖N + 1 - Z3)✖N + 1 - Z4 magic Hipercube (6 dim.): ((((MA = TM✖N + 1 - Z1)✖N + 1 - Z2)✖N + 1 - Z3)✖N + 1 - Z4)✖N + 1 - Z5 notic: mainmatrix MA, submatrix Z1, Z2, Z3. Z4, Z5, order N, ✖ multiplication sign. Visualization of dynamic processes here in almost polar system is extraordinary and beautiful. To see them please click on the individual graphic and scroll down. |
Z1-string in simple inalid overlapping group 1 squares of order 69 |
||
Strings in the pandiagonal magic squares in almost polar system |
TM-string in irregular pandiagonal magic squares of order 29 |
||
Analyse all methods of the symmetrics magis squares order 19 |